Mathematics-Stationary Points

In mathematical calculus, stationary point is an input to a function where the first derivative of a function or slope of function is zero( i.e., dy / dx = 0 ). dy / dx called derivative of y or slope of the function y = f( x ). In stationary point function stops increasing or decreasing.

A stationary point may be maximum or minimum or inflection point.
Eg::) y = f ( x ) = x²
       dy / dx = 2x 
       Stationary point locates at when 2x = 0 or dy / dx = 0.Minimum stationary point is the stationary point at which gradient is -ve just before the minimum, and zero , and +ve just after the minimum.

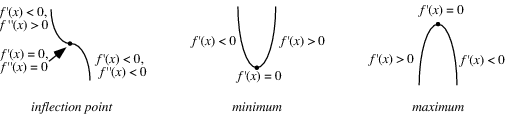
Maximum stationary point is the stationary point at which gradient is +ve just before the maximum, and zero , and -ve just after the maximum.

In Point of inflection, gradient can be +ve, 0, +ve or -ve, 0, -ve

Eg::) Find stationary point on the graph y = x² + 2x³ and mention its nature.
         Here, y = x² + 2x³ 

         dy / dx = 2x + 6x² 

         At stationary points, dy / dx = 0

         So (  2x + 6x²  ) = 0, 2x ( 1+3x ) = 0

         x = 0, -1 / 3

         when x = 0, y = 0 and when x = -1 / 3 , y = 1 / 27

         Find the gradient at either side of zero.

         When x = -0.01, dy / dx = -ve,

         x = 0, dy / dx = 0

         x = +0.01, dy / dx = +ve

         So it shows the minimum stationary point. 
          
         Find the gradient at either side of -1/3

         When x = -0.3334, dy / dx = +ve,

         x = -0.3333, dy / dx = 0

         x = -0.3332, dy  / dx = -ve

         So it shows the maximum stationary point. 

So minimum stationary point at ( 0, 0 ) and maximum stationary point at (-1 / 3, 1 / 27 ) .